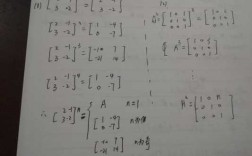本篇目录:
- 1、如何判别牛顿迭代法收敛性?
- 2、...内,当r在(2,3)区间内时,如何证明迭代序列{Xn}是收敛的?
- 3、证明迭代格式收敛性可以是开区间吗
- 4、迭代矩阵与收敛定理
- 5、迭代矩阵收敛定理
- 6、证明:若矩阵A为对称正定阵,且0ω2,则解线性方程组AX=b的逐次超松弛...
如何判别牛顿迭代法收敛性?
1、收敛条件可以通过比较迭代步骤之间的差异来判定,如果差异小于一定的阈值,则可以认为收敛已经发生。这种收敛条件可以有效地控制算法的收敛速度,从而提高算法的效率。
2、全局收敛性是指初值在定义域内任取时算法是否收敛,若收敛其速度如何,收敛到哪个根.具体来说。

3、局部收敛性定理:假设问题解存在,断定当初始近似与解充分接近时迭代法收敛。半局部收敛性定理:在不假定解存在的情况下,根据迭代法在初始近似处满足的条件,断定迭代法收敛于问题的解。
...内,当r在(2,3)区间内时,如何证明迭代序列{Xn}是收敛的?
所以p点位于三条直线形成的三角形内。x+y即为点p到原点的距离的平方,也可以看做以原点为圆心的圆的半径的平方。所以由图像可以很轻易的知道(1/2,1/2)点离原点最近,(1,1)点离原点最远。
数列收敛则数列必然有界,但是反过来不一定成立!例如:Xn=1,-1,1,-1,...|Xn|=1,是有界的,但是Xn不收敛。
全局收敛 对于任意的X0∈[a,b],由迭代式Xk+1=φ(Xk)所产生的点列收敛,即其当k→∞时,Xk的极限趋于X*,则称Xk+1=φ(Xk)在[a,b]上收敛于X*。

有界函数指的是对于定义域中的任意一个值,相应的函数值都在一个区间内变化,也就是函数值的绝对值总小于某一个固定值,那函数就是有界的。
证明迭代格式收敛性可以是开区间吗
1、因此,收敛域有可能是开区间(即两个端点都是发散的),有可能是半闭半开区间(即在闭合点处收敛),有可能是全闭合区间(即两个端点都是收敛的)。
2、迭代解法的收敛性意味着它能够在有限的步骤内收敛到最优解,从而节省时间和资源。收敛条件可以通过比较迭代步骤之间的差异来判定,如果差异小于一定的阈值,则可以认为收敛已经发生。
3、它基于函数的连续性和单调性来证明函数的收敛性。

4、收敛区间是个开区间,而收敛域就是判断在收敛区间的端点上是否收敛。譬如说求出一个级数的收敛半径为5那么此时收敛区间为(-5,5)而下一步求收敛域就带x=-5和x=5,分别看是否收敛。
5、《数值分析》9迭代法收敛性条件迭代误差估计定理13:301/34总结:矩阵范数算子范数算子范数矩阵1范数,矩阵无穷范数,矩阵2范数2/34例4设.为Rn×n上任意一种矩阵范数,则对任意的A∈Rn×n,有(A)A。
6、迭代算法的敛散性 全局收敛 对于任意的X0∈[a,b],由迭代式Xk+1=φ(Xk)所产生的点列收敛,即其当k→∞时,Xk的极限趋于X*,则称Xk+1=φ(Xk)在[a,b]上收敛于X*。
迭代矩阵与收敛定理
1、★定理五:松弛迭代格式(5-14)收敛的必要条件为0ω2。★定理六:若A为正定矩阵,则当0ω2时,松弛迭代格式(5-14)恒收敛。显然正定方程组的G-S迭代法必收敛(因为ω=1)。
2、★定理二:若方程组Ax=b的系数矩阵A,满足下面条件中任何一条,则J-迭代收敛。
3、★定理三:若方程组系数矩阵A为按行或列对角占优,则其G-S迭代法收敛。★定理四:若方程组系数矩阵A为正定矩阵,则其G-S迭代法收敛。
4、Jacobi迭代收敛,因此当|a|4时,一定是收敛的.不过要注意,这是个收敛的充分条件,不是必要条件. 这里的newton 法是求方程f(x)=0的根的方法。
5、局部收敛性定理:假设问题解存在,断定当初始近似与解充分接近时迭代法收敛。半局部收敛性定理:在不假定解存在的情况下,根据迭代法在初始近似处满足的条件,断定迭代法收敛于问题的解。
迭代矩阵收敛定理
★定理三:若方程组系数矩阵A为按行或列对角占优,则其G-S迭代法收敛。★定理四:若方程组系数矩阵A为正定矩阵,则其G-S迭代法收敛。
★定理二:若方程组Ax=b的系数矩阵A,满足下面条件中任何一条,则J-迭代收敛。
ek就是度量迭代序列{xk}与真解之间的距离,ek=0表示已经得到真解。 可以证明,f(x)满足一定的条件,则{xk}二次收敛到x*,大致上说就是 ek约为e(k-1)^2,这是一个收敛很快的方法。
迭代法 x[n+1] = x[n] - f(x[n])/f(x[n])得到的序列 x[n] 总收敛到a,且收敛速度至少是二阶的。若 f(a) == 0(多重零点),则初值取在a的某个邻域内时,收敛速度是一阶的。
局部收敛性定理:假设问题解存在,断定当初始近似与解充分接近时迭代法收敛。半局部收敛性定理:在不假定解存在的情况下,根据迭代法在初始近似处满足的条件,断定迭代法收敛于问题的解。
普半径小于1,则收敛,否则不收敛。其中谱半径就是迭代矩阵J或者G的最大特征值。也可用列范数或行范数判断,列范数或者行范数小于1,则收敛。但范数大于1时,不能说明其发散,还要通过计算谱半径来确定其收敛性。
证明:若矩阵A为对称正定阵,且0ω2,则解线性方程组AX=b的逐次超松弛...
对于逐次超松弛迭代法,松弛因子的选取对算法的收敛速度有很大影响,通常对于方程组Ax=Y,若A为正定矩阵,则当0w 2时,逐次超松弛迭代恒收敛。
但由于收敛速度缓慢,使计算量变得很大而失去使用价值。是为了解决大规模系统的线性等式提出,松弛因子的选取对算法的收敛速度有很大影响,通常对于方程组Ax=Y,若A为正定矩阵,当02时,逐次超松弛迭代恒收敛。
非齐次线性方程组AX=b 有唯一解;A的行(列)向量组线性无关;任一n维向量可由A的行(列)向量组线性表示。
到此,以上就是小编对于如何证明迭代法收敛的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏